Observera att detta avsnitt handlar om konceptet grader endast med en naturlig indikator och noll.

Begreppet och egenskaperna hos grader med rationella exponenter (med negativa och bråktal) kommer att diskuteras i lektioner för årskurs 8.

Så låt oss ta reda på vad en grad av ett tal är. För att skriva produkten av ett tal för sig själv används den förkortade notationen flera gånger.

Istället för att multiplicera sex identiska faktorer 4 4 4 4 4 4 skriver de 4 6 och säger "fyra till sjätte potens".

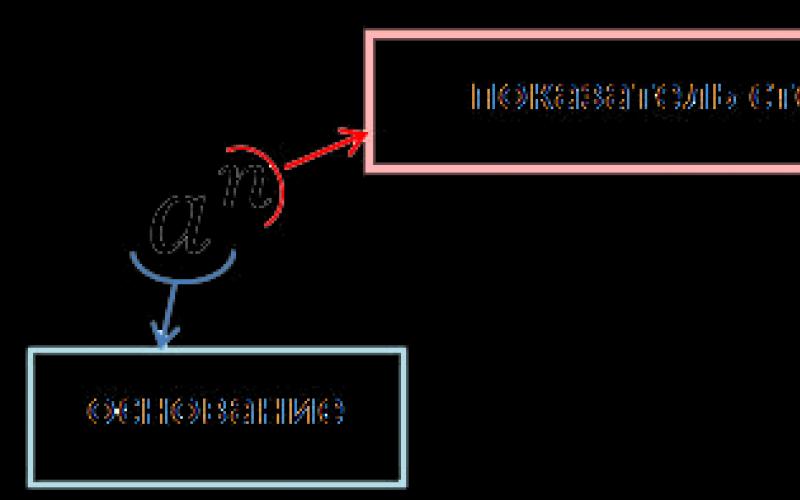
4 4 4 4 4 4 = 4 6

Uttrycket 4 6 kallas potensen av ett tal, där:

• 4 — examensbas;
• 6 — exponent.

I allmänhet skrivs graden med basen "a" och exponenten "n" med hjälp av uttrycket:

Kom ihåg!

Graden av talet "a" med en naturlig exponent" n",större än 1, är produkten" n»Identiska faktorer, som var och en är lika med talet "a".

Posten "a n"Det lyder så här:" och till potensen n "eller" n:te potensen av talet a".

Undantagen är posterna:

• a 2 - det kan uttalas som "en kvadrat";
• a 3 - det kan uttalas som "a i en kub."

• a 2 - "och till andra graden";
• a 3 - "a till tredje graden."

Specialfall uppstår om exponenten är lika med ett eller noll (n = 1; n = 0).

Kom ihåg!

Graden av talet "a" med exponenten n \u003d 1 är detta tal i sig:
a 1 = a

Varje tal till nollpotensen är lika med ett.
a 0 = 1

Noll till någon naturlig kraft är lika med noll.
0 n = 0

En till valfri makt är lika med 1.
1n=1

Uttryck 0 0 ( noll till noll effekt) anses meningslöst.

• (−32) 0 = 1
• 0 253 = 0
• 1 4 = 1

När du löser exempel måste du komma ihåg att att höja till en potens kallas att hitta ett numeriskt eller bokstavligt värde efter att ha höjt det till en potens.

Exempel. Höj till en makt.

• 5 3 = 5 5 5 = 125
• 2,5 2 = 2,5 2,5 = 6,25
• ( · = = 81

  256

Exponentiering av ett negativt tal

Potensens bas (talet som höjs till en potens) kan vara vilket tal som helst - positivt, negativt eller noll.

Kom ihåg!

Att höja ett positivt tal till en potens resulterar i ett positivt tal.

Att höja noll till en naturlig effekt resulterar i noll.

När man höjer ett negativt tal till en potens kan resultatet vara antingen ett positivt tal eller ett negativt tal. Det beror på om exponenten var ett jämnt eller udda tal.

Tänk på exempel på att höja negativa tal till en potens.

Det kan ses från de övervägda exemplen att om ett negativt tal höjs till en udda potens så erhålls ett negativt tal. Eftersom produkten av ett udda antal negativa faktorer är negativ.

Om ett negativt tal höjs till en jämn potens, erhålls ett positivt tal. Eftersom produkten av ett jämnt antal negativa faktorer är positiv.

Kom ihåg!

Ett negativt tal upphöjt till en jämn potens är ett positivt tal.

Ett negativt tal upphöjt till en udda potens är ett negativt tal.

Kvadraten av ett tal är ett positivt tal eller noll, det vill säga:

a 2 ≥ 0 för valfritt a .

• 2 (−3) 2 = 2 (−3) (−3) = 2 9 = 18
• −5 (−2) 3 = −5 (−8) = 40

Notera!

När man löser exponentieringsexempel görs ofta misstag, man glömmer bort att posterna (−5) 4 och −5 4 är olika uttryck. Resultaten av att höja till en makt av dessa uttryck kommer att bli annorlunda.

Beräkna (−5) 4 betyder att hitta värdet av fjärde potensen av ett negativt tal.

(−5) 4 = (−5) (−5) (−5) (−5) = 625

Att hitta "-5 4" betyder att exemplet måste lösas i två steg:

1. Höj den positiva siffran 5 till fjärde potens.
   5 4 = 5 5 5 5 = 625
2. Sätt ett minustecken framför det erhållna resultatet (det vill säga utför en subtraktionsåtgärd).
   −5 4 = −625

Exempel. Beräkna: −6 2 − (−1) 4

−6 2 − (−1) 4 = −37

1. 6 2 = 6 6 = 36
2. −6 2 = −36
3. (−1) 4 = (−1) (−1) (−1) (−1) = 1
4. −(−1) 4 = −1
5. −36 − 1 = −37

Procedur för exempel med examina

Att beräkna ett värde kallas exponentieringsåtgärden. Detta är det tredje steget.

Kom ihåg!

I uttryck med grader som inte innehåller parentes, utför först exponentiering, då multiplikation och division, och i slutet addition och subtraktion.

Om det finns parenteser i uttrycket, utförs först, i den ordning som anges ovan, åtgärderna inom parenteser och sedan de återstående åtgärderna i samma ordning från vänster till höger.

Exempel. Beräkna:

För att underlätta lösningen av exempel är det användbart att känna till och använda gradtabellen som du kan ladda ner gratis på vår hemsida.

För att kontrollera dina resultat kan du använda kalkylatorn på vår hemsida "

Exponentiering är en operation som är nära relaterad till multiplikation, denna operation är resultatet av multipel multiplikation av ett tal i sig själv. Låt oss representera formeln: a1 * a2 * ... * an = an.

Till exempel, a=2, n=3: 2 * 2 * 2=2^3 = 8 .

I allmänhet används exponentiering ofta i olika formler inom matematik och fysik. Denna funktion har ett mer vetenskapligt syfte än de fyra grundläggande: Addition, Subtraktion, Multiplikation, Division.

Att höja ett nummer till en makt

Att höja ett nummer till en makt är inte en svår operation. Det är relaterat till multiplikation som förhållandet mellan multiplikation och addition. Spela in en - en kort post av det n:te antalet siffror "a" multiplicerat med varandra.

Överväg exponentiering på de enklaste exemplen, gå vidare till komplexa.

Till exempel, 42. 42 = 4 * 4 = 16 . Fyra i kvadrat (till andra potensen) är lika med sexton. Om du inte förstår multiplikationen 4 * 4, läs då vår artikel om multiplikation.

Låt oss titta på ett annat exempel: 5^3. 5^3 = 5 * 5 * 5 = 25 * 5 = 125 . Fem kuber (till tredje potens) är lika med hundra tjugofem.

Ett annat exempel: 9^3. 9^3 = 9 * 9 * 9 = 81 * 9 = 729 . Nio tärningar är lika med sjuhundratjugonio.

Exponentieringsformler

För att korrekt höja till en potens måste du komma ihåg och känna till formlerna nedan. Det finns inget utöver det naturliga i detta, det viktigaste är att förstå essensen och då kommer de inte bara att komma ihåg, utan också verka lätta.

Att höja en monomial till en makt

Vad är en monomial? Detta är produkten av siffror och variabler i valfri kvantitet. Till exempel är två en monomial. Och den här artikeln handlar om att höja sådana monomer till en makt.

Med hjälp av exponentieringsformler kommer det inte att vara svårt att beräkna exponentieringen av en monomial till en potens.

Till exempel, (3x^2y^3)^2= 3^2 * x^2 * 2 * y^(3 * 2) = 9x^4y^6; Om du höjer en monomial till en potens, så höjs varje komponent i monomialen till en potens.

När man höjer en variabel som redan har en grad till en potens multipliceras graderna. Till exempel, (x^2)^3 = x^(2 * 3) = x^6 ;

Att höja sig till en negativ makt

En negativ exponent är den reciproka av ett tal. Vad är ett ömsesidigt? För vilket nummer X som helst är den reciproka 1/X. Det är X-1=1/X. Detta är kärnan i den negativa graden.

Tänk på exemplet (3Y)^-3:

(3Y)^-3 = 1/(27Y^3).

Varför är det så? Eftersom det finns ett minus i graden överför vi helt enkelt detta uttryck till nämnaren och höjer det sedan till tredje potens. Precis rätt?

Höjning till en bråkdel makt

Låt oss börja med ett specifikt exempel. 43/2. Vad betyder makt 3/2? 3 - täljare, betyder att höja ett tal (i detta fall 4) till en kub. Talet 2 är nämnaren, detta är extraheringen av den andra roten av talet (i detta fall 4).

Då får vi kvadratroten ur 43 = 2^3 = 8 . Svar: 8.

Så, nämnaren för en bråkdelgrad kan vara antingen 3 eller 4, och i oändlighet vilket tal som helst, och detta tal bestämmer graden av kvadratroten extraherad från ett givet tal. Naturligtvis kan nämnaren inte vara noll.

Att höja en rot till en makt

Om roten höjs till en makt lika med rotens kraft, så är svaret det radikala uttrycket. Till exempel, (√x)2 = x. Och så i alla fall av likhet mellan graden av roten och graden av att höja roten.

Om (√x)^4. Sedan (√x)^4=x^2. För att kontrollera lösningen översätter vi uttrycket till ett uttryck med bråkgrad. Eftersom roten är kvadratisk är nämnaren 2. Och om roten höjs till fjärde potens så är täljaren 4. Vi får 4/2=2. Svar: x = 2.

I vilket fall som helst är det bästa alternativet att helt enkelt konvertera uttrycket till en bråkdelsexponent. Om bråket inte reduceras, kommer ett sådant svar att bli, förutsatt att roten av det givna talet inte allokeras.

Exponentiering av ett komplext tal

Vad är ett komplext tal? Ett komplext tal är ett uttryck som har formeln a + b * i; a, b är reella tal. i är talet som i kvadrat ger talet -1.

Tänk på ett exempel. (2 + 3i)^2.

(2 + 3i)^2 = 22 +2 * 2 * 3i +(3i)^2 = 4+12i^-9=-5+12i.

Anmäl dig till kursen "Få snabbare mentalräkning, INTE huvudräkning" för att lära dig hur du snabbt och korrekt adderar, subtraherar, multiplicerar, dividerar, kvadrattal och till och med slår rötter. På 30 dagar kommer du att lära dig hur du använder enkla knep för att förenkla aritmetiska operationer. Varje lektion innehåller nya tekniker, tydliga exempel och användbara uppgifter.

Exponentiering online

Med hjälp av vår kalkylator kan du beräkna exponentieringen av ett tal till en potens:

Exponentieringsbetyg 7

Att höja sig till en makt börjar passera skolbarn först i sjunde klass.

Exponentiering är en operation som är nära relaterad till multiplikation, denna operation är resultatet av multipel multiplikation av ett tal i sig själv. Låt oss representera formeln: a1 * a2 * … * an=an .

Till exempel, a=2, n=3: 2 * 2 * 2 = 2^3 = 8.

Exempel på lösningar:

Exponentieringspresentation

Presentation om exponentiering, designad för sjundeklassare. Presentationen kan förtydliga några obegripliga punkter, men det kommer förmodligen inte att finnas sådana punkter tack vare vår artikel.

Resultat

Vi har bara övervägt toppen av isberget, för att förstå matematiken bättre - anmäl dig till vår kurs: Påskynda mentalräkning - INTE huvudräkning.

Från kursen kommer du inte bara att lära dig dussintals knep för förenklad och snabb multiplikation, addition, multiplikation, division, räkna ut procentsatser, utan också arbeta fram dem i specialuppgifter och pedagogiska spel! Mental räkning kräver också mycket uppmärksamhet och koncentration, som aktivt tränas i att lösa intressanta problem.

I fortsättningen på samtalet om graden av ett tal är det logiskt att syssla med att hitta gradens värde. Denna process har fått ett namn exponentiering. I den här artikeln kommer vi bara att studera hur exponentiering utförs, medan vi kommer att beröra alla möjliga exponenter - naturliga, heltals, rationella och irrationella. Och av tradition kommer vi att i detalj överväga lösningarna på exempel på att höja siffror i olika grader.

Sidnavigering.

Vad betyder "exponentiering"?

Låt oss börja med att förklara vad som kallas exponentiering. Här är den relevanta definitionen.

Definition.

Exponentieringär att hitta värdet av potensen av ett tal.

Att hitta värdet av potensen av a med exponenten r och höja talet a till potensen av r är alltså samma sak. Till exempel, om uppgiften är "beräkna värdet av potensen (0,5) 5", kan den omformuleras enligt följande: "Höj talet 0,5 till potensen 5".

Nu kan du gå direkt till reglerna för exponentiering.

Att höja ett nummer till en naturlig kraft

I praktiken tillämpas oftast jämställdhet utifrån i formen . Det vill säga, när man höjer talet a till en bråkpotens m/n, extraheras först roten av n:te graden från talet a, varefter resultatet höjs till en heltalspotts m.

Överväg lösningar på exempel på att höja till en bråkdel.

Exempel.

Beräkna värdet på graden.

Lösning.

Vi visar två lösningar.

Första sättet. Per definition av grad med en bråkdelsexponent. Vi beräknar värdet på graden under rotens tecken, varefter vi extraherar kubroten: .

Det andra sättet. Genom definition av en grad med bråkexponent och på basis av egenskaperna hos rötterna är likheterna sanna . Extrahera nu roten Slutligen höjer vi till en heltalspotens .

Uppenbarligen sammanfaller de erhållna resultaten av att höja till en bråkdel.

Svar:

Observera att bråkexponenten kan skrivas som ett decimalbråk eller ett blandat tal, i dessa fall ska det ersättas med motsvarande ordinarie bråktal, och sedan ska exponentiering utföras.

Exempel.

Beräkna (44,89) 2,5 .

Lösning.

Vi skriver exponenten i form av en vanlig bråkdel (om nödvändigt, se artikeln): . Nu utför vi höjning till en bråkdel:

Svar:

(44,89) 2,5 =13 501,25107 .

Det bör också sägas att höjning av tal till rationella potenser är en ganska mödosam process (särskilt när täljaren och nämnaren för bråkexponenten är ganska stora tal), som vanligtvis utförs med hjälp av datorteknik.

Som avslutning av detta stycke kommer vi att uppehålla oss vid konstruktionen av talet noll till en bråkpotens. Vi gav följande betydelse till bråkgraden noll i formen: för vi har , medan noll till effekten m/n inte är definierad. Så, noll till en positiv bråkpotens är noll, till exempel, . Och noll i en negativ bråkpotens är inte vettigt, till exempel är uttrycken och 0 -4,3 inte vettiga.

Att höja sig till en irrationell makt

Ibland blir det nödvändigt att ta reda på värdet på graden av ett tal med en irrationell exponent. I det här fallet räcker det av praktiska skäl oftast att få fram examensvärdet upp till ett visst tecken. Vi noterar direkt att detta värde i praktiken beräknas med hjälp av elektronisk datorteknik, eftersom manuell höjning till en irrationell effekt kräver ett stort antal besvärliga beräkningar. Men inte desto mindre kommer vi att i allmänna termer beskriva essensen av handlingarna.

För att få ett ungefärligt värde på exponenten av a med en irrationell exponent, tas en viss decimal approximation av exponenten, och värdet på exponenten beräknas. Detta värde är det ungefärliga värdet av graden av talet a med en irrationell exponent. Ju mer exakt decimal approximationen av talet tas initialt, desto mer exakt blir gradvärdet i slutändan.

Som ett exempel, låt oss beräkna det ungefärliga värdet av potensen 2 1,174367... . Låt oss ta följande decimalapproximation av en irrationell indikator: . Nu höjer vi 2 till en rationell makt på 1,17 (vi beskrev kärnan i denna process i föregående stycke), vi får 2 1,17 ≈ 2,250116. På det här sättet, 2 1,174367... ≈2 1,17 ≈2,250116 . Om vi ​​tar en mer exakt decimal approximation av en irrationell exponent, till exempel, , får vi ett mer exakt värde på den ursprungliga graden: 2 1,174367... ≈2 1,1743 ≈2,256833 .

Bibliografi.

• Vilenkin N.Ya., Zhokhov V.I., Chesnokov A.S., Shvartsburd S.I. Matematik Zh lärobok för 5 celler. läroinstitut.
• Makarychev Yu.N., Mindyuk N.G., Neshkov K.I., Suvorova S.B. Algebra: en lärobok för 7 celler. läroinstitut.
• Makarychev Yu.N., Mindyuk N.G., Neshkov K.I., Suvorova S.B. Algebra: lärobok för 8 celler. läroinstitut.
• Makarychev Yu.N., Mindyuk N.G., Neshkov K.I., Suvorova S.B. Algebra: en lärobok för 9 celler. läroinstitut.
• Kolmogorov A.N., Abramov A.M., Dudnitsyn Yu.P. Algebra och början av analys: En lärobok för årskurserna 10-11 av allmänna utbildningsinstitutioner.
• Gusev V.A., Mordkovich A.G. Matematik (en manual för sökande till tekniska skolor).

Vi räknade ut vad graden av ett tal är i allmänhet. Nu måste vi förstå hur man korrekt beräknar det, d.v.s. höja siffrorna till makter. I detta material kommer vi att analysera de grundläggande reglerna för att beräkna graden i fallet med en heltal, naturlig, bråkdel, rationell och irrationell exponent. Alla definitioner kommer att illustreras med exempel.

Begreppet exponentiering

Låt oss börja med formuleringen av grundläggande definitioner.

Definition 1

Exponentieringär beräkningen av värdet av potensen av något tal.

Det vill säga orden "beräkning av gradens värde" och "exponentiering" betyder samma sak. Så om uppgiften är "Höj talet 0 , 5 till femte potensen", bör detta förstås som "beräkna värdet på potensen (0 , 5) 5 .

Nu ger vi de grundläggande reglerna som måste följas i sådana beräkningar.

Kom ihåg vad en potens av ett tal med en naturlig exponent är. För en potens med bas a och exponent n blir detta produkten av det n:te antalet faktorer, som var och en är lika med a. Detta kan skrivas så här:

För att beräkna gradens värde måste du utföra multiplikationsoperationen, det vill säga multiplicera baserna för graden det angivna antalet gånger. Själva konceptet med en examen med en naturlig indikator bygger på förmågan att snabbt föröka sig. Låt oss ge exempel.

Exempel 1

Skick: Höj - 2 till styrkan 4 .

Lösning

Med hjälp av definitionen ovan skriver vi: (− 2) 4 = (− 2) (− 2) (− 2) (− 2) . Därefter behöver vi bara följa dessa steg och få 16 .

Låt oss ta ett mer komplicerat exempel.

Exempel 2

Beräkna värdet 3 2 7 2

Lösning

Det här inlägget kan skrivas om till 3 2 7 · 3 2 7 . Tidigare har vi tittat på hur man korrekt multiplicerar de blandade talen som nämns i villkoret.

Utför dessa steg och få svaret: 3 2 7 3 2 7 = 23 7 23 7 = 529 49 = 10 39 49

Om uppgiften indikerar behovet av att höja irrationella tal till en naturlig kraft, måste vi först avrunda deras baser till en siffra som gör att vi kan få ett svar med önskad noggrannhet. Låt oss ta ett exempel.

Exempel 3

Utför kvadreringen av talet π .

Lösning

Låt oss avrunda det till hundradelar först. Sedan π 2 ≈ (3, 14) 2 = 9, 8596. Om π ≈ 3 . 14159, då får vi ett mer exakt resultat: π 2 ≈ (3, 14159) 2 = 9, 8695877281.

Observera att behovet av att beräkna potenserna av irrationella tal i praktiken uppstår relativt sällan. Vi kan sedan skriva svaret som själva potensen (ln 6) 3 eller konvertera om möjligt: ​​5 7 = 125 5 .

Separat bör det anges vad den första potensen av ett tal är. Här kan du bara komma ihåg att varje nummer som höjs till första potensen kommer att förbli sig själv:

Detta framgår av journalen. .

Det beror inte på examen.

Exempel 4

Så, (− 9) 1 = − 9 , och 7 3 upphöjda till första potensen förblir lika med 7 3 .

För enkelhetens skull kommer vi att analysera tre fall separat: om exponenten är ett positivt heltal, om det är noll och om det är ett negativt heltal.

I det första fallet är detta detsamma som att höja till en naturlig kraft: trots allt hör positiva heltal till mängden naturliga tal. Vi har redan beskrivit hur man arbetar med sådana grader ovan.

Låt oss nu se hur man korrekt höjer till nolleffekten. Med en bas som inte är noll ger denna beräkning alltid en utdata på 1 . Vi har tidigare förklarat att 0:e potensen av a kan definieras för vilket reellt tal som helst som inte är lika med 0, och a 0 = 1.

Exempel 5

5 0 = 1 , (- 2 , 56) 0 = 1 2 3 0 = 1

0 0 - ej definierad.

Vi har bara fallet med en grad med en negativ heltalsexponent. Vi har redan diskuterat att sådana grader kan skrivas som en bråkdel 1 a z, där a är vilket tal som helst och z är ett negativt heltal. Vi ser att nämnaren för detta bråk inte är något annat än en vanlig grad med ett positivt heltal, och vi har redan lärt oss hur man beräknar det. Låt oss ge exempel på uppgifter.

Exempel 6

Höj 2 till -3-effekten.

Lösning

Med hjälp av definitionen ovan skriver vi: 2 - 3 = 1 2 3

Vi beräknar nämnaren för denna bråkdel och får 8: 2 3 \u003d 2 2 2 \u003d 8.

Då är svaret: 2 - 3 = 1 2 3 = 1 8

Exempel 7

Höj 1, 43 till -2-effekten.

Lösning

Omformulera: 1 , 43 - 2 = 1 (1 , 43) 2

Vi räknar ut kvadraten i nämnaren: 1,43 1,43. Decimaler kan multipliceras på detta sätt: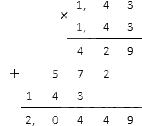

Som ett resultat fick vi (1, 43) - 2 = 1 (1, 43) 2 = 1 2 , 0449 . Det återstår för oss att skriva detta resultat i form av ett vanligt bråk, för vilket det är nödvändigt att multiplicera det med 10 tusen (se materialet om omvandling av bråk).

Svar: (1, 43) - 2 = 10000 20449

Ett separat fall är att höja ett nummer till minus första potens. Värdet på en sådan grad är lika med talet motsatt basens ursprungliga värde: a - 1 \u003d 1 a 1 \u003d 1 a.

Exempel 8

Exempel: 3 − 1 = 1 / 3

9 13 - 1 = 13 9 6 4 - 1 = 1 6 4 .

Hur man höjer en siffra till en bråkpotens

För att utföra en sådan operation måste vi komma ihåg den grundläggande definitionen av en grad med en bråkdelsexponent: a m n \u003d a m n för varje positivt a, heltal m och naturligt n.

Definition 2

Således måste beräkningen av en bråkgradig grad utföras i två steg: höjning till en heltalspotens och hitta roten till den n:e graden.

Vi har likheten a m n = a m n , som, givet rötternas egenskaper, vanligtvis används för att lösa problem i formen a m n = a n m . Det betyder att om vi höjer talet a till en bråkpotens m / n, så extraherar vi först roten av n:e graden från a, sedan höjer vi resultatet till en potens med en heltalsexponent m.

Låt oss illustrera med ett exempel.

Exempel 9

Beräkna 8 - 2 3 .

Lösning

Metod 1. Enligt den grundläggande definitionen kan vi representera detta som: 8 - 2 3 \u003d 8 - 2 3

Låt oss nu beräkna graden under roten och extrahera den tredje roten från resultatet: 8 - 2 3 = 1 64 3 = 1 3 3 64 3 = 1 3 3 4 3 3 = 1 4

Metod 2. Låt oss omvandla den grundläggande jämlikheten: 8 - 2 3 \u003d 8 - 2 3 \u003d 8 3 - 2

Därefter extraherar vi roten 8 3 - 2 = 2 3 3 - 2 = 2 - 2 och kvadrerar resultatet: 2 - 2 = 1 2 2 = 1 4

Vi ser att lösningarna är identiska. Du kan använda hur du vill.

Det finns fall då graden har en indikator uttryckt som ett blandat tal eller decimalbråk. För att underlätta beräkningen är det bättre att ersätta det med en vanlig bråkdel och räkna enligt ovan.

Exempel 10

Höj 44,89 till styrkan 2,5.

Lösning

Låt oss omvandla värdet på indikatorn till en vanlig bråkdel: 44 , 89 2 , 5 = 44 , 89 5 2 .

Och nu utför vi alla åtgärder som anges ovan i ordning: 44 , 89 5 2 = 44 , 89 5 = 44 , 89 5 = 4489 100 5 = 4489 100 5 = 67 2 10 2 5 = 67 10 5 01 = 01 = 01 = 01 13 501, 25107

Svar: 13501, 25107.

Om det finns stora tal i täljaren och nämnaren för en bråkdelsexponent, är det ett ganska svårt jobb att beräkna sådana exponenter med rationella exponenter. Det kräver vanligtvis datorteknik.

Separat uppehåller vi oss vid graden med en nollbas och en bråkdelsexponent. Ett uttryck av formen 0 m n kan ges följande betydelse: om m n > 0, då 0 m n = 0 m n = 0 ; om m n< 0 нуль остается не определен. Таким образом, возведение нуля в дробную положительную степень приводит к нулю: 0 7 12 = 0 , 0 3 2 5 = 0 , 0 0 , 024 = 0 , а в целую отрицательную - значения не имеет: 0 - 4 3 .

Hur man höjer ett nummer till en irrationell makt

Behovet av att beräkna värdet på graden, i vars indikator det finns ett irrationellt tal, uppstår inte så ofta. I praktiken är uppgiften vanligtvis begränsad till att beräkna ett ungefärligt värde (upp till ett visst antal decimaler). Detta beräknas vanligtvis på en dator på grund av komplexiteten i sådana beräkningar, så vi kommer inte att uppehålla oss i detalj, vi kommer bara att ange de viktigaste bestämmelserna.

Om vi ​​behöver beräkna värdet av graden a med en irrationell exponent a , så tar vi exponentens decimalapproximation och räknar från den. Resultatet blir ett ungefärligt svar. Ju mer exakt decimal approximation som tas, desto mer exakt är svaret. Låt oss visa med ett exempel:

Exempel 11

Beräkna det ungefärliga värdet av 2 i potensen 1,174367....

Lösning

Vi begränsar oss till decimalapproximationen a n = 1 , 17 . Låt oss göra beräkningarna med detta tal: 2 1 , 17 ≈ 2 , 250116 . Om vi ​​till exempel tar approximationen a n = 1 , 1743 , så blir svaret lite mer exakt: 2 1 , 174367 . . . ≈ 2 1. 1743 ≈ 2. 256833 .

Om du märker ett fel i texten, markera det och tryck på Ctrl+Enter

Vi påminner dig om att vi förstår den här lektionen examensegenskaper med naturliga indikatorer och noll. Examina med rationella indikatorer och deras egenskaper kommer att diskuteras på lektionerna för årskurs 8.

En exponent med en naturlig exponent har flera viktiga egenskaper som gör att du kan förenkla beräkningar i exponentexempel.

Fastighet #1
Produkt av makter

Kom ihåg!

När potenser multipliceras med samma bas förblir basen oförändrad och exponenterna adderas.

a m a n \u003d a m + n, där "a" - vilket tal som helst och "m", "n" - alla naturliga tal.

Denna egenskap hos potenser påverkar också produkten av tre eller flera potenser.

• Förenkla uttrycket.
  b b 2 b 3 b 4 b 5 = b 1 + 2 + 3 + 4 + 5 = b 15
• Presenteras som examen.
  6 15 36 = 6 15 6 2 = 6 15 6 2 = 6 17
• Presenteras som examen.
  (0,8) 3 (0,8) 12 = (0,8) 3 + 12 = (0,8) 15

Viktig!

Observera att det i den angivna egenskapen endast handlade om att multiplicera potenser med samma grunder . Det gäller inte deras tillägg.

Du kan inte ersätta summan (3 3 + 3 2) med 3 5 . Detta är förståeligt om
beräkna (3 3 + 3 2) = (27 + 9) = 36 och 3 5 = 243

Fastighet #2
Privata examina

Kom ihåg!

När man dividerar potenser med samma bas förblir basen oförändrad, och divisorns exponent subtraheras från exponenten för utdelningen.

= 11 3 − 2 4 2 − 1 = 11 4 = 44

Exempel. Lös ekvationen. Vi använder egenskapen partiella grader.
3 8: t = 3 4

T = 3 8 − 4

Svar: t = 3 4 = 81

Med hjälp av egenskaper nr 1 och nr 2 kan du enkelt förenkla uttryck och utföra beräkningar.

• Exempel. Förenkla uttrycket.
  4 5m + 6 4 m + 2: 4 4m + 3 = 4 5m + 6 + m + 2: 4 4m + 3 = 4 6m + 8 − 4m − 3 = 4 2m + 5
• Exempel. Hitta värdet på ett uttryck med hjälp av gradegenskaper.
  = = = 2 9 + 2

  2 5

  = 2 11

  2 5

  = 2 11 − 5 = 2 6 = 64

  Viktig!

  Observera att fastighet 2 endast handlade om maktdelning med samma grunder.

  Du kan inte ersätta skillnaden (4 3 −4 2) med 4 1 . Detta är förståeligt om vi överväger (4 3 −4 2) = (64 − 16) = 48 och 4 1 = 4

  Var försiktig!

  Fastighet #3
  Exponentiering

  Kom ihåg!

  När man höjer en potens till en potens förblir basen för potensen oförändrad, och exponenterna multipliceras.

  (a n) m \u003d a n m, där "a" är valfritt tal och "m", "n" är alla naturliga tal.

  
  

  Egenskaper 4
  Produktexamen

  Kom ihåg!

  När man höjer en produkt till en makt, höjs var och en av faktorerna till en makt. Resultaten multipliceras sedan.

  (a b) n \u003d a n b n, där "a", "b" är alla rationella tal; "n" - vilket naturligt tal som helst.

  • Exempel 1
    (6 a 2 b 3 c) 2 = 6 2 a 2 2 b 3 2 s 1 2 = 36 a 4 b 6 s 2
    
  • Exempel 2
    (−x 2 y) 6 = ((−1) 6 x 2 6 y 1 6) = x 12 y 6

  Viktig!

  Observera att egenskap nr 4, liksom andra egenskaper för grader, också tillämpas i omvänd ordning.

  (a n b n)= (a b) n

  Det vill säga, för att multiplicera potenser med samma exponenter kan du multiplicera baserna och lämna exponenten oförändrad.

  • Exempel. Beräkna.
    2 4 5 4 = (2 5) 4 = 10 4 = 10 000
  • Exempel. Beräkna.
    0,5 16 2 16 = (0,5 2) 16 = 1

  I mer komplexa exempel kan det finnas fall då multiplikation och division måste utföras på potenser med olika baser och olika exponenter. I det här fallet rekommenderar vi att du gör följande.

  Till exempel, 4 5 3 2 = 4 3 4 2 3 2 = 4 3 (4 3) 2 = 64 12 2 = 64 144 = 9216
  

  Exempel på exponentiering av ett decimaltal.

  4 21 (−0,25) 20 = 4 4 20 (−0,25) 20 = 4 (4 (−0,25)) 20 = 4 (−1) 20 = 4 1 = 4

  Egenskaper 5
  Kvotens makt (bråk)

  Kom ihåg!

  För att höja en kvot till en potens kan du höja utdelningen och divisorn separat till denna potens och dividera det första resultatet med det andra.

  (a: b) n \u003d a n: b n, där "a", "b" är alla rationella tal, b ≠ 0, n är vilket naturligt tal som helst.

  • Exempel. Uttryck uttrycket som partiella makter.
    (5: 3) 12 = 5 12: 3 12

  Vi påminner om att en kvot kan representeras som en bråkdel. Därför kommer vi att uppehålla oss vid ämnet att höja en bråkdel till en makt mer detaljerat på nästa sida.

---